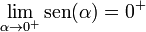Sistema De Medición De Ángulos
Si la rotación del lado terminal es en sentido contrario al de las agujas del reloj, la
medida del ángulo será positiva, en caso contrario la medida será negativa.
El sistema sexagesimal, cuya unidad es el grado: º
Y el sistema radial cuya unidad es el radián: rad
DEFINICIÓN:
Un grado sexagesimal es la medida del ángulo, con
vértice en el centro de un círculo, de amplitud igual
a la 360 ava parte del mismo.
Si el lado terminal realiza una
rotación completa, en el sentido
contrario de las agujas del reloj, el
ángulo generado mide 360º.
DEFINICIÓN:
Un radián es la medida del ángulo con vértice en el
centro de un círculo de radio r, cuyos lados
determinan sobre la circunferencia un arco AB de
longitud igual al radio
Si el lado lt realiza una
rotación completa en
sentido positivo, el ángulo
generado mide 2p radianes
Recuerda que, el cociente entre la longitud
de una circunferencia y la medida de su
diámetro no depende de la circunferencia
con la que se trabaje. El cociente es
constante.
Ese número es el número p !!
Por lo tanto: p
2longitud radio
longitud circunferencia
para ver la explicación de clic aquí
EJEMPLOS
EJERCICIOS
Dibuja en un mismo sistema de ejes en forma exacta un ángulo de
45º y uno de 405º¿qué observación puedes hacer?
Llamaremos ángulos coterminales a aquellos que, en posición normal, tienen lados
terminales coincidentes.
1- ¿Cuántos grados mide, aproximadamente, un ángulo de 1 radián?
2- Convierte a grados la medida del ángulo que en el sistema radial mide p 7/6
-
3- Convierte a radianes el ángulo que en el sistema sexagesimal mide 20º
Rtas: 1- 57º
2- 210º
3-ñ / 9 radianes
LONGITUD DE UN ARCO DE CIRCUNFERENCIA
A partir de la definición de la medida de un ángulo en radianes, vimos que ar =
r
long AB
por lo tanto long AB = r ar.
OBSERVACIÓN
Esta fórmula es válida sólo si a está
medido en radianes!
1- Determina la longitud del arco generado por un ángulo de 2 radianes
en una circunferencia de radio r = 4cm.
2- Idem si el ángulo mide 45º y la circunferencia es de radio r = 2cm.
3- Determina la medida del ángulo correspondiente a un arco de 6,9 cm
de longitud subtendido en una circunferencia de radio r = 3 cm.
4- Una milla marítima se define como la longitud del arco subtendido en
la superficie de la Tierra por un ángulo que mide 1 minuto. El
diámetro de la Tierra es aproximadamente 7.927 millas (terrestres).
Determina la cantidad de millas (terrestres) que hay en una milla
marítima.
RECUERDA
Longitud de la circunferencia = p . diámetro Superficie lateral de la esfera =
= p .(diámetro )
2
Área del círculo = p . (radio )
2
Volumen de la esfera =
= 4 / 3 . p .(radio)
3
p = 3.141 592 653 5...
.









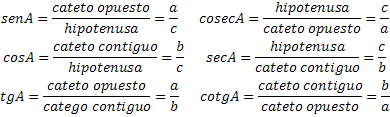





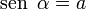
 proviene del latín sĭnus.
proviene del latín sĭnus.


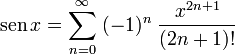

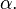
 con el valor del coseno del ángulo de amplitud, expresada en
con el valor del coseno del ángulo de amplitud, expresada en 






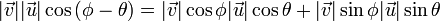




 :
:

 :
:



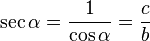



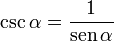

 .
.

 .
.