| En términos de | 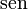 |  |  |  |  |  |
|---|---|---|---|---|---|---|
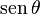 | 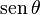 | 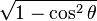 |  |  | 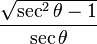 |  |
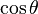 | 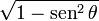 | 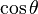 |  | 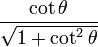 |  | 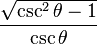 |
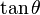 |  | 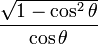 |  | 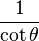 |  |  |
 |  |  |  | 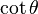 |  |  |
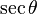 | 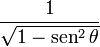 | 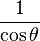 | 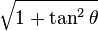 | 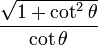 | 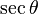 |  |
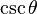 | 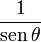 | 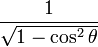 |  |  |  | 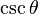 |
De las definiciones de las funciones trigonométricas:
Son más sencillas de probar en la circunferencia trigonométrica o goniométrica (que tiene radio igual a 1):
A veces es importante saber que cualquier combinación lineal de una serie de ondas senoidales que tienen el mismo período pero están desfasadas, es también una onda senoidal del mismo período pero con un desplazamiento de fase diferente. Dicho de otro modo:
Es llamada identidad trigonométrica fundamental, y efectuando sencillas operaciones permite encontrar unas 24 identidades más, muy útiles para problemas introductorios del tipo conocido el valor de la función seno, obtenga el valor de las restantes (sin tabla ni calculadora).
Por ejemplo, si se divide ambos miembros de "sen² + cos² = 1" por cos², se obtiene:
Ahora, dividiendo ambos miembros de la misma expresión por el sen², se obtiene:
Entonces puede expresarse la función seno según alguna otra conocida:
Ejemplo 2:
Utilizando la identidad
Entonces:
Pero
sustituimos en 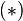 :
:
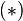 :
:
Realizamos las operaciones necesarias y queda:
Entonces los cosenos se hacen 1 y queda
Y queda demostrado.
El resto de las funciones se realiza de manera análoga.
Ejemplos



TALLER


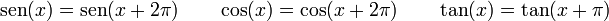



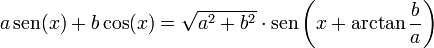
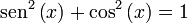


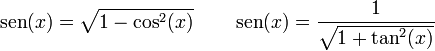

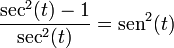

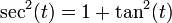
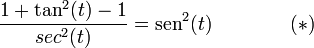
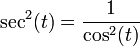


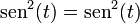
No hay comentarios:
Publicar un comentario