Funsion Del Seno:
En trigonometría el seno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto opuesto y la hipotenusa:
O también como la ordenada correspondiente a un punto que pertenece a una circunferencia unitaria centrada en el origen (c=1):
En matemáticas el seno es la función obtenida al hacer variar la razón mencionada, siendo una de las funciones trascendentes. La abreviatura  proviene del latín sĭnus.
proviene del latín sĭnus.
 proviene del latín sĭnus.
proviene del latín sĭnus.
Ejemplos:

TALLER:
Función De Coseno:
En trigonometría el coseno (abreviado cos) de un ángulo agudo en un triángulo rectángulo se define como la razón entre el cateto adyacente a ese ángulo y la hipotenusa:
En virtud del Teorema de Tales, este número no depende del triángulo rectángulo escogido y, por lo tanto, está bien construido y define una función del ángulo 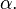
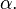
Otro modo de obtener el coseno de un ángulo consiste en representar éste sobre la circunferencia goniométrica, es decir, la circunferencia unitaria centrada en el origen. En este caso el valor del coseno coincide con la abscisa del punto de intersección del ángulo con la circunferencia. Esta construcción es la que permite obtener el valor del coseno para ángulos no agudos.
En análisis matemático el coseno es la función que asocia un número real  con el valor del coseno del ángulo de amplitud, expresada en radianes,
con el valor del coseno del ángulo de amplitud, expresada en radianes,  . Es una función trascendente y analítica, cuya expresión en serie de potencias es
. Es una función trascendente y analítica, cuya expresión en serie de potencias es
 con el valor del coseno del ángulo de amplitud, expresada en radianes,
con el valor del coseno del ángulo de amplitud, expresada en radianes,  . Es una función trascendente y analítica, cuya expresión en serie de potencias es
. Es una función trascendente y analítica, cuya expresión en serie de potencias es
- Utilizando las dos definiciones de producto escalar se obtiene:
- Por igualación se define que
- Las componentes de los vectores se pueden reemplazar como la proyección de su módulo sobre los ejes, es decir
- Reemplazando esta propiedad en ambos vectores nos queda
- Extrayendo como factor común los módulos de los vectores en el segundo miembro
TALLER:
Ver taller
Función Tangente:
En trigonometría la tangente de un ángulo en un triángulo rectángulo se define como la razón entre el cateto opuesto y el adyacente:
Definición de tangente de un ángulo agudo:
Sea A un ángulo agudo de un triángulo rectángulo. La tangente del ángulo A es el cociente entre el cateto opuesto BC y el adyacente AB.
La tangente en la circunferencia goniométrica.
Se llama circunferencia goniométrica a la que tiene su centro en el origen de coordenadas y de radio uno.
Cualquier punto de la circunferencia dista 1 del origen, por lo tanto, si representamos el ángulo con el vértice en el origen de coordenadas y un lado sobre el semieje OXpositivo, el valor de la tangente coincide con la ordenada del punto cuya abcisa vale uno (ya que, entonces, el denominador vale 1).
Observa que el segmento que obtenemos es tangente a la circunferencia goniométrica.
Click aquí para ver explicación completa
Ejemplos:
Esta identidad trigonométrica parte de la identidad de la suma de dos ángulos ya conocida para el seno y el coseno.
- Dados los ángulos
 :
:
- Reemplazando por las identidades antes mencionadas:
- Dividiendo al numerador y al denominador por
 :
:
- Separando la suma y la resta:
Ver mas ejemplos
TALLER:
clic aquí para ver el taller completo
Función Del Cotangente
La cotangente, abreviado como cot, cta, o cotg, es la razón trigonométrica inversa de la tangente, o también su inverso multiplicativo:Dom f=R-,
Ran f= R
Periodo: π.

para ver mas explicación clic aquí
Ejemplos
La función cotangente asocia a cada número real, x, el valor de la cotangente del ángulo cuya medida en radianes es x.
f(x) = cotx

TALLER
clic aqui para ver el taller
Función Del Secante
El Secante, (abreviado como sec), es la razón trigonométrica inversa del coseno, o también su inverso multiplicativo:

clic aquí para ver la explicación completa
Ejemplos
Partiendo de la definición de secante como la inversa del coseno:
Función cosecante
La Cosecante (abreviado como csc o cosec) es la razón trigonométrica inversa del seno, o también su inverso multiplicativo:

clic aqui para ver mas explicacion
Ejemplos
Partiendo de la definición de cosecante como la inversa del seno:
Y conociendo la función seno previamente, podemos ver que para los valores en los que el seno vale cero, la cosecante se hace infinito, si la función seno tiende a cero desde valores negativos la cosecante tiende a:  .
.
 .
.
mientras que cuando el seno tiende a cero desde valores positivos la cosecante tiende a:  .
.
 .
.
Cuando el seno del ángulo vale uno, su cosecante también vale uno, como se puede ver en la gráfica.

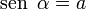








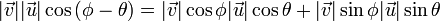









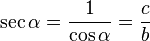



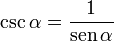



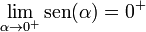

no le entiendo ni madres
ResponderEliminary reprobare por tu culpa u.u
que pena
EliminarTampoco entiendo nada, muchas gracias me quedare con el 5 por tu explicación demasiado explícita.
EliminarPerfecto copia y pega de la Wikipedia?
ResponderEliminarpues creo que tengo lo que necesito, no entiendo mucho pero gracias!
ResponderEliminarQue kk
ResponderEliminar